1 海量存储系统的体系结构

存储系统在高速度、大容量、低成本三者之间是存在矛盾的。在追求单个存储器高性能的同时，通过先进的体系结构技术，可以构建出性价比最优的复合存储系统。

  • 海量存储系统的研究目标： 通过软硬件结合、本地与网络结合的方法，研究新型体系结构技术，设计出性能优化的存储系统。

  • 概括： 将不同容量、速度、价格的存储器组成多层系统，通过软硬件组合为整体，数据分布在各层中，达到最优化的性能价格比。从cpu的角度上看，这个多级存储系统具有与最快存储器相当的速度，容量相当于磁盘的高速、大容量存储器，每字节成本接近磁盘。

    1.1 多级存储层次的基本概念

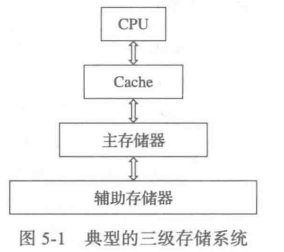
    在这里插入图片描述

在存储系统多级层次结构中，由上至下分为三级，容量递增，速度递减，成本递减。整体又分为两个层次

  • Cache-主存层次：
    在这里插入图片描述

  • 主存-辅存层次：
    在这里插入图片描述

    • 进一步细分，先进的CPU内部含有三级存储体系，分别是寄存器、L1 Cache、L2 Cache:

    在这里插入图片描述

    • 多级结构存储系统服从两个基本原则：
      在这里插入图片描述
      存储层次结构的有效性基于实践局部性、空间局部性两个局部性原理：

  • 时间局部性（Temproral Locality） ：如果某个数据或指令被引用，那么不久后它可能再次被引用。将最近访问的数据项保存在离微处理器最接近的地方，最近的时间范围内被使用的可能性很大。

  • 空间局部性（Spatial Locality） ： 如果某个数据或指令被引用，那么地址邻近的数据或指令和可能不久也将被引用。以由地址连续的若干字构成的块为单位，从低层复制到上一层，它们被使用的概率极大。
    在这里插入图片描述

    1.2 多级存储层次的性能分析

    常用术语：

  • 块 Block ： 相邻两级间数据交换的单位；
  • 命中和命中率 h ：命中指CPU产生的有效地址可以直接在高层存储器中访问到，其概率成为命中率；
  • 不命中率m ：m=1-h；
  • 命中时间 $t_h$ : 访问高层存储器所需的时间，包括判定本次访问是否命中的时间；
  • 不命中时间 $t_m$：用底层存储器中相应的块替换高层存储器中的块，并将所访问的数据传送到请求访问的设备的时间。$t_m$由访问时间和传送时间两部分组成;
  • 访问时间 ：指缺失时在底层存储器中访问到块中第一个字的时间，与底层存储器的延迟有关；
  • 传送时间 ：传送块内字所需的时间，与两级之间的带宽及块大小有关；

命中率与硬件速度无关，与应用程序的行为特性有关，采用以下参数来评价存储器层次结构的特性：
二级存储结构：M1和M2，其中M1比M2高一级，它们的位价格，容量，访问时间分别为：$c_1,s_1,t_{a1}；c_2,s_2,t_{a2}$。

  • 每位的平均价格 $c=\frac{c_1s_1+c_2s_2}{s_1+s_2}$;
  • 命中率（hit ratio）$h = \frac{N_1}{N_1+N_2}$,其中在一组访问中，有N1次在M1中访问到数据，N2次在M2中访问到数据；不命中率（miss ratio）$m=\frac{N_2}{N_1+N_2}$;
  • 命中时间$t_h=t_{a1}$，不命中时的访问时间$t_m=t_{a2}+t_b$。因为$t_{a1}+t_{a2}+t_b=t_{a1}+t_m$为不命中时总的时间开销，其中$t_b$是从M2传送一个数据块到M1的时间开销。
  • 平均访存时间 ：
    $T_A=ht_{a1}+(1-h)(t_{a1}+t_m)=t_{a1}+(1-h)*t_m$；
    可见在命中率h无限接近1的时候，平均访存时间就是M1的访存时间。