cmu445-5 Hash Table
讨论如何支持DBMS执行引擎从页中读写数据。主要涉及两种数据结构:
- Hash Tables
- Trees
Data Structure
DBMS为系统内部的许多不同部分使用不同的数据结构:
Internal Meta-Data:
跟踪有关数据库和系统状态的信息
Core Data Storage:
可用作数据库中的元组的基本存储器
Temporary Data Structure:
DBMS可以在处理查询时动态地构建数据结构,以加快执行速度(例如,连接的哈希表)
Table Indexes:
辅助数据结构,使它更容易找到特定的元组
设计决策:
- 数据组织:我们如何布局内存,以及在数据结构中存储的信息。
- 并发性:如何使多个线程能够访问数据结构而不会引起问题。
Hash Table
哈希表实现了一个将键映射到值的关联数组抽象数据类型。它提供了平均操作复杂性和存储复杂度。
哈希表的实现可以分为两个部分:
Hash Function:
如何将一个很大的地址空间映射到一个更小的域,将索引通过计算映射到一个桶数组或者slot。需要在计算速度与哈希碰撞率之间进行权衡。
Hashing Scheme:
如何处理哈希过后的键值碰撞,需要在分配大哈希表以减少碰撞和执行额外指令以查找/插入键值之间进行权衡。
Hash Functions
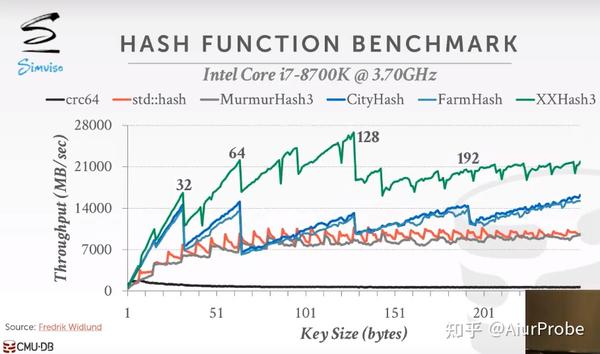
DBMS不希望使用加密哈希函数(例如,SHA-256),因为我们不需要担心保护密钥的内容。这些散列函数主要由DBMS内部使用,因此信息不会泄露到系统之外。对于本讲座,我们只关心哈希函数的速度和碰撞率。目前最先进的哈希函数是Facebook XXHash3。
| 名称 | 特点 |
|---|---|
| CRC-64(1975) | 应用在网络中进行差错监测,慢 |
| MurmurHash(2008) | 被设计成为一种快速、通用的哈希函数 |
| Google CityHash(2001) | 对小键值运行更快 |
| Facebook XXHash(2012) | 诞生自zstd压缩 |
| Google FarmHash(2014) | 对CityHash的碰撞率进行优化 |
Static Hashing Schemes
静态哈希方案是一种固定哈希表大小的方案。这意味着,如果DBMS耗尽了散列表中的存储空间,那么它必须用一个较大的表从头重新构建它。通常,新的哈希表的大小是原始哈希表的两倍。
Linear Probe Hashing
这是最基本的哈希方案。它通常也是最快的。它使用一个插槽表。散列函数允许DBMS快速跳转到插槽中,并寻找所需的键。
插入时: 当发现需要插入的slot已存在其他key时, 就沿某个方向线性地查找, 直到找到一个空的slot
查找时: 当发现经过hash运算得到的slot并未保存待查的key时, 沿某个方向线性查找, 直到找到正确的slot
删除时: 不能将该slot置空, 而应设置一个墓碑标记(tombstone)
- 墓碑标记: 该标记表示这个位置曾经保存过key, 如果想要在这个位置插入是没问题的. 如果在查找时hash到了这个位置, 应该继续向某个方向线性查找; 如果不设置这个标记, 查找时hash到这个位置, 发现是空的, 那么查找器是直接返回”哈希表中不存在这个key”, 还是需要沿着某个方向把整张表挨个查一遍才能确定是否存在这个key? 设置该标记后, 遇到标记则跳过, 继续线性探测, 遇到真正的空slot就可得知哈希表中确实不存在这个key
Non-unique Keys:当一个多个value对应的key相同,常见的方法是Redundant Keys,即将重复的键值项一起存放在哈希表中,查找某一key对应的所有键值对时一直扫描知道遇到空的slot,这种方法可能会造成空间浪费但是总体可接受。
Robin Hood Hashin
该策略基于线性探测法, 目标是在全局上让每个key需要探测才能插入(找到)的探测步数都少一些(而不是偏爱某些key). 探测的步数越多, 即这个key离它应该在的位置越远, 这个key越”poor”, 反之则”rich”。当poor的key想要插入rich的key所在的slot时, rich的key就需要”挪挪位置”, 力求”平等富裕”。
从整体上看, 这样更加平衡. 虽然这会在插入时带来更高的写入代价(窃取别人位置时要把别人赶走), 但如果哈希表更多被用来读的话这样做就是值得的
不过现代有研究表明, 当使用罗宾汉法大量插入key时, 由于要判断更多的条件才能决定插入的位置, 并且可能要写很早以前用过的数据, 可能导致大量缓存失效/分支预测失败, 极端场景下综合性能不如简单的线性探测。
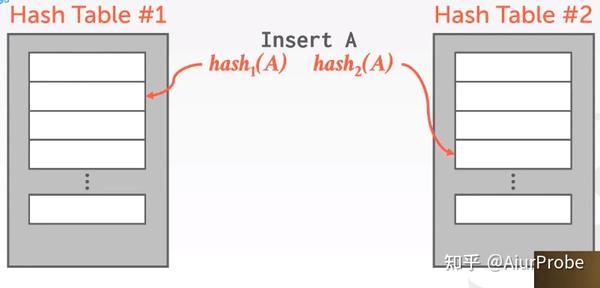
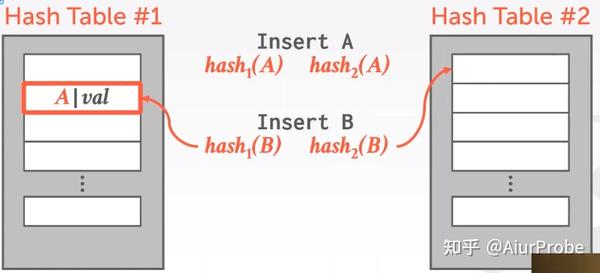
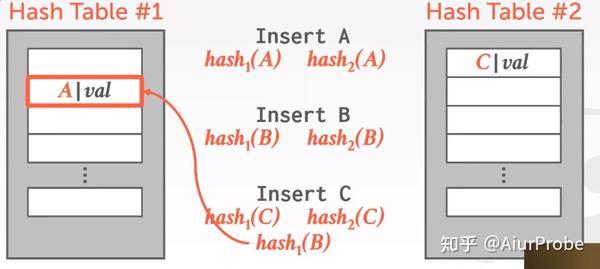
Cuckoo Hashing
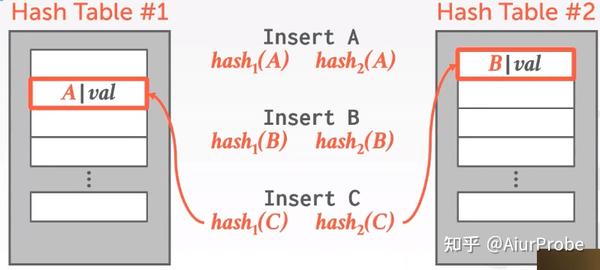
这种策略使用多个(大多数情况下是2个)哈希表, 用更高的写入代价换取查询和删除都是O(1)。这种策略会产生递归碰撞的问题, 如果所有的碰撞形成了一个闭环, 那这些蛋就会在巢之间永远移来移去. 为了解决这个问题, 需要记录碰撞的起始点, 当发现碰了一圈都没能把所有的key安顿好时, 说明哈希表需要扩容了.
 |
 |
 |
|---|---|---|
 |
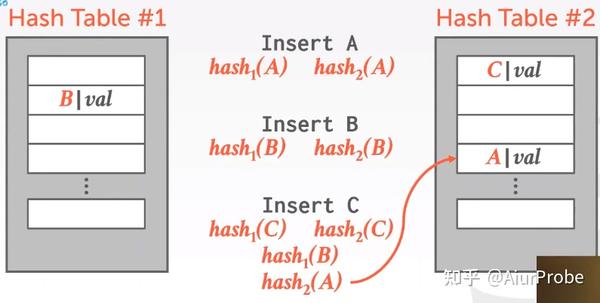 |
可以发现, 以这种策略安顿好的所有的key, 都呆在hash function直接为它指出的两个slot中的一个, 因此查找和删除都是O(1)的。
Dynamic Hashing Schemes
动态策略不需要提前预估key的规模, 也能够在无需重建整个哈希表的情况下根据需要调整大小。
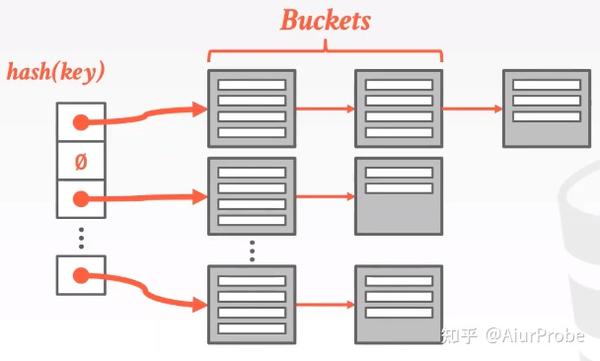
Chained Hashing
即链地址法: 将slot中保存的value变成一个指向bucket链表的指针, 当得到相同的hash结果时, 不再在大哈希表中大量线性查找, 而是去自家链表里探测. (至于链表什么时候转为红黑树请参考其他资料) . 链表能够无限扩容下去。在极端情况下将变为线性查找。
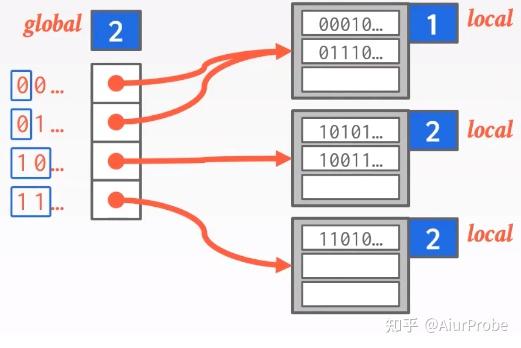
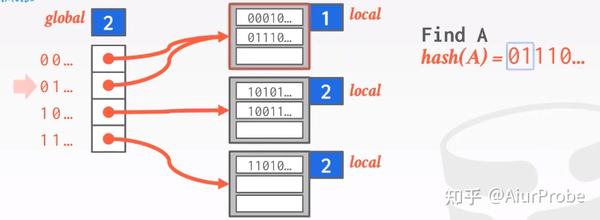
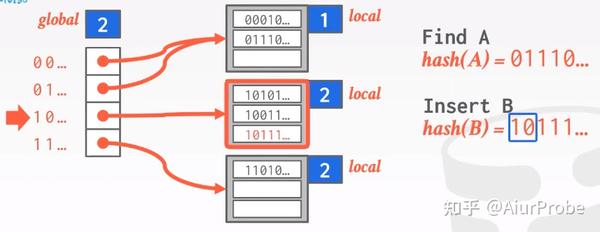
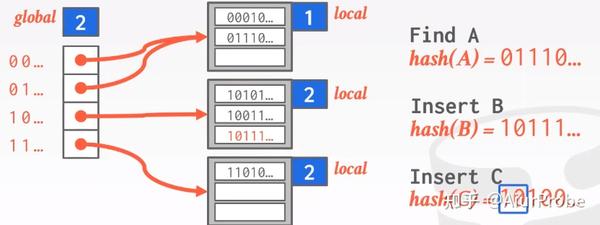
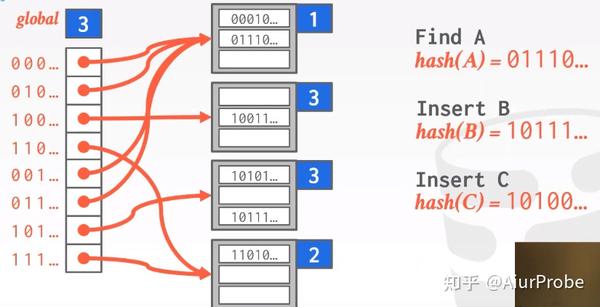
Extendible Hashing
这种方法也用bucket处理一些碰撞, 但与链地址法不同的是, 它不是在每个bucket后面简单粗暴地无限扩容下去, 而是用“局部重建”的思路处理bucket溢出。整个方法有一个global变量, 标识着hash function的结果总要取前多少个bit; 每个bucket有一个local变量, 标识着hash function的结果需要看几个bit, 就可以确定填入本bucket。如果该策略应用在磁盘存储上, 左侧的global数组保存的就是page id, 而右边的每个bucket则是一个page。
 |
 |
 |
|---|---|---|
 |
 |
Linear Hashing
前述的Extendible Hashing策略有一个问题就是每次扩容, 左侧的数组空间都要翻倍(因为需要多计算一位), 这个操作计算量虽然不大, 但是在扩容完成前, 这个数组都是要被latch锁住的(因为需要重新分配指向关系), 在锁住期间没有线程能访问整个hash table, 这个问题在高并发场景下就会成为性能瓶颈。
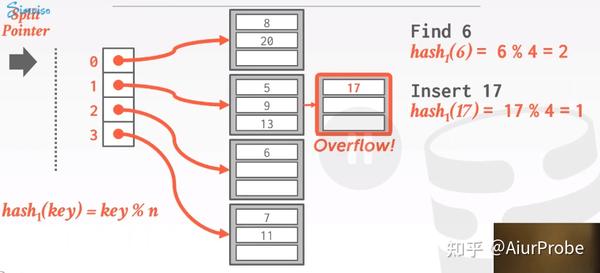
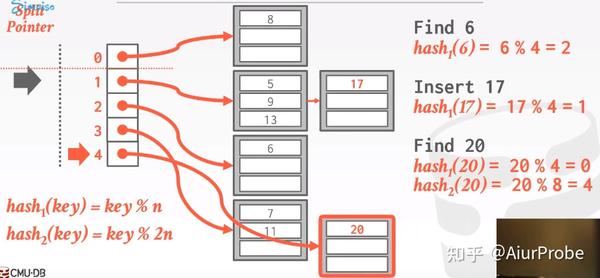
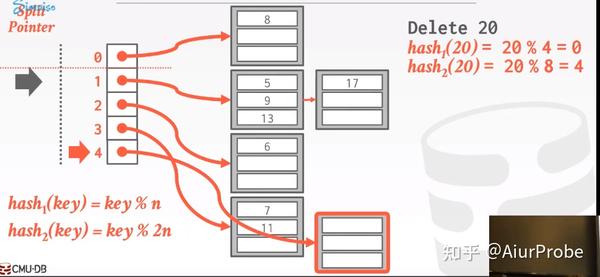
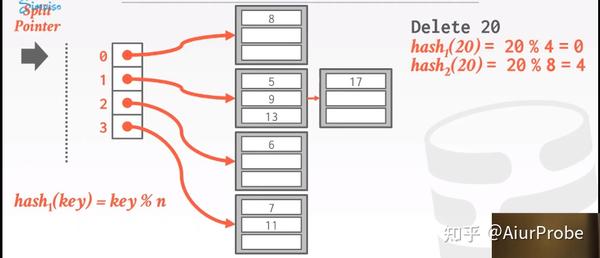
Linear Hashing策略的思路就是只需要重新分配溢出的bucket, 从而削弱这个问题的影响. 它基于链地址法。该策略维护一个Split Pointer全局变量指针, 用于指示下次扩容应该拆分哪个bucket. 无论下次需要扩容时该bucket是否已满, 都必须拆分该指针指向的bucket。
 |
 |
|---|---|
 |
 |





