cmu445-6 Tree Indexes

Indexes

table index是数据columns子集的复制，允许DBMS可以比顺序扫描更快的查找tuple。DBMS保证数据表的内容和索引内容同步。对于指定查询，选择哪一种索引以使得查询执行的更快是DBMS来完成的。建立索引需要额外的存储开销，也需要维护，所以每个数据库创建的索引数量需要trade-off。

B+Tree

定义：

自平衡，每个叶子节点所处高度一致
除叶子节点外每个节点至少满足: $\frac{M}{2} − 1 <= num\ of\ keys <= M − 1$
每个具有k个关键字的内部节点都具有k+1个孩子

B+树中的每个节点都包含一个键/值对的数组：

每个节点上的数组（几乎）都是按键进行排序的
内部节点的值数组将包含指向其他节点的指针
对于叶子节点指向的具体的值value，有两种处理方式：
- Record IDs: 保存一个指向tuple地址的指针
- Tuple Data: tuple的真实内容在叶子节点中排序存放

B+树的插入删除操作网上资料很丰富，https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html该网站可以动画模拟B+树的操作

B+Tree Design Decisions

节点大小：

B个+树的最佳节点大小取决于磁盘的速度。其想法是将尽可能多的将键/值对从磁盘读取节点到内存以摊销成本
磁盘越慢，节点大小应该越大
相对于大量点查询，有些工作负载可能更偏向于scan操作

合并策略：

有些DBMS在节点处于half full的情况下并不会合并节点
延迟节点合并可能会减少数据重新组织的次数
允许某些节点处于underflow状态然后周期性地重建整棵树可能有利于DBMS

可变长度的键：

常见的方法是使用Key Map，在节点内部嵌入一个指向key+value列表的指针。和之前讨论的slotted page类似。

非唯一性索引：

使用Duplicate Keys：将key替换为key+RecordId，RecordId=pageId+offset of slot。因为物理位置互不相同，相同的key也能够比较大小了。缺点是需要保存的东西更多了，需要消耗更多空间存储索引。
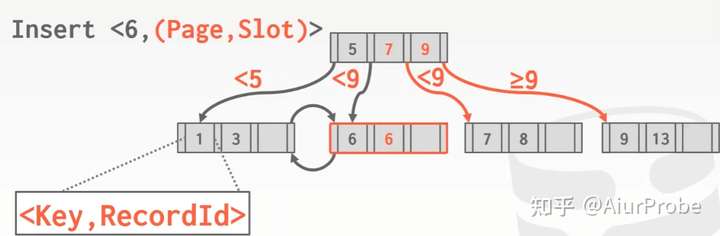
使用Value Lists：

简单地扩展叶子结点，将相同的key存储进溢出区中。缺点是这会打破B+树的平衡限制，使结点内的key由有序变为无序，查找时找到了叶子结点也要线性扫描所有该结点下挂着的溢出区。比如要查找的key为6，那么找到第二层后需要依次扫描6->7->8->6->7->6，才能不遗漏。

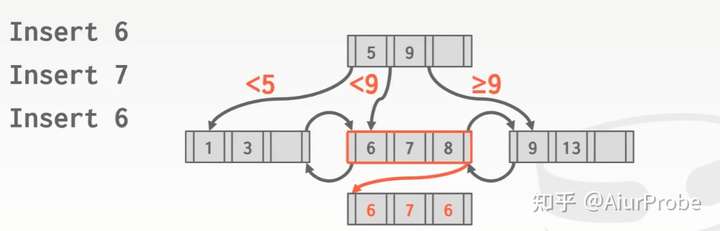
节点内搜索策略：

线性搜索：从头到尾扫描节点中的键/值条目。当你找到你要找的 key 时，停下来。这不需要对键/值条目进行预排序。
二分搜索：跳到中间 key，然后根据中间关键字小于还是大于搜索关键字向左/向右旋转。这需要对键/值条目进行预排序。
插值 Interpolation：根据节点中已知的低/高关键字值，近似计算搜索关键字的起始位置。然后从该位置执行线性扫描。这需要对键/值条目进行预排序。

B+Tree Optimizations

prefix compression 前缀压缩

因为key都是排好序的，所以可能会出现大量重复的前缀。记录它们的公共前缀而不是重复地存储完整的key，会节省大量的存储空间。
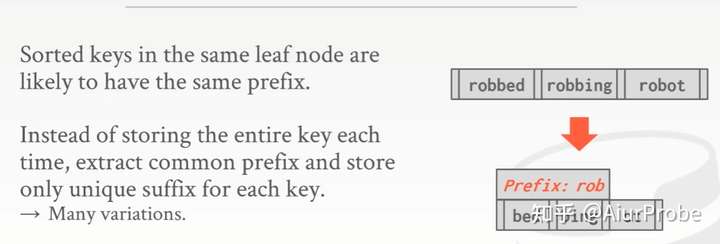
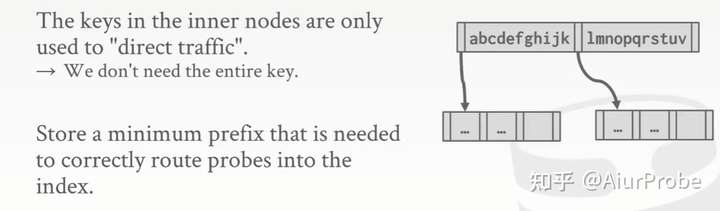
suffix truncation 后缀截断

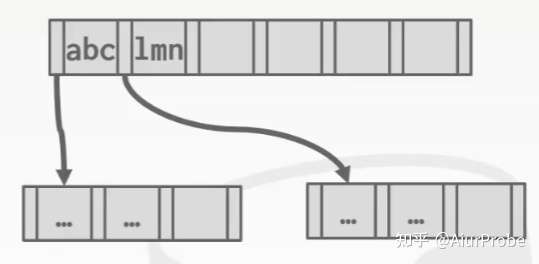
当用于确认方向的路标很长，但是迥然不同时，也没有必要存完整的key，abcdefg…存储为abc，lmnopq…存储为lmn即可。这种方式在树不会经常改变时很有用，总体上用的比前缀压缩要少。
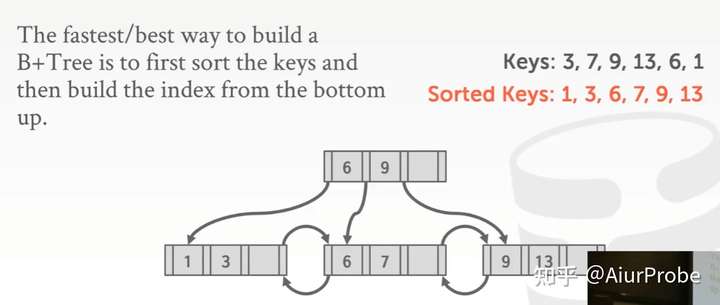
Bulk Inserts：当提前知道需要插入的所有key时，可以预先对key们排序，然后自下而上地构建整颗树，这样比逐次插入快很多。
pointer swizzling

当确保需要遍历的结点所在的page都被pin在buffer pool中时，结点间指针就不用再(仅)存page id，而是可以直接(额外)存原始指针，遍历这些node时就能避免去访问buffer pool的时延。这个技术 (Pointer swizzling - Wikipedia) 的本意是由于持久化保存(链表等数据结构的)指针逻辑地址没有意义，因为把逻辑地址写到磁盘里，预计之后按原样拼起来，但是再读出来的时候逻辑地址就什么也不是了，所以保存下一个node的id而不是地址值充当指针的作用，这个操作叫unswizzling。在数据库中反其道而行之，如果DBMS确保都会在内存里操作，就可以专门存地址的原始值而不是page id。因为树的高层结点使用频率非常高，它们pin在buffer pool里是常见的事情，这个技术使用场景比较多。

Additional Index Usage

隐式索引（Implicit Indexes）：大多数DBMS会自动创建索引来实施完整性约束(例如，主键、唯一约束)。

部分索引（Partial Indexes）：在整个表的子集上创建索引，（where语句形成子集）。这可能会减少大小和维护开销。

覆盖索引（Covering Indexes）：处理查询所需的所有属性都在索引中可用，则DBMS不需要检索元组。DBMS只需根据索引中可用的数据即可完成整个查询。（即，索引的数据中就能满足本次查找，不需要再去检索元组了，无需回表操作）

索引包含列（Index Include Columns）：在索引中嵌入其他列以支持仅索引查询。

函数/表达式索引（Function/Expression Indexes）：将函数或表达式的输出存储为键，而不是原始值。DBMS的工作是识别哪些查询可以使用该索引。

Radix Tree

一个 radix tree 是 Trie数据结构的变体。它使用 key 的 digital\ 表示来逐个检查前缀，而不是比较整个 key 。它与trie的不同之处在于，key 中的每个元素都没有一个节点，在key不同之前，节点被合并以表示最大的前缀。

Radix tree 的高度取决于 key 的长度，而不是像B+树那样取决于 key 的数量。指向叶节点的路径表示叶的关键字。并非所有属性类型都可以分解为基数树的二进制可比数字。

对于长整型数据的映射，如何解决Hash冲突和Hash表大小的设计是一个很头疼的问题。

radix树就是针对这种稀疏的长整型数据查找，能快速且节省空间地完成映射。借助于Radix树，我们可以实现对于长整型数据类型的路由。利用radix树可以根据一个长整型（比如一个长ID）快速查找到其对应的对象指针。这比用hash映射来的简单，也更节省空间，使用hash映射hash函数难以设计，不恰当的hash函数可能增大冲突，或浪费空间。

Radix tree是一种多叉搜索树，树的叶子结点是实际的数据条目。每个结点有一个固定的、2^n指针指向子结点（每个指针称为槽slot，n为划分的基的大小）

Trie树一般用于字符串到对象的映射，Radix树一般用于长整数到对象的映射。