Tim Kraska、Jeffrey Dean等人在SIGMOD 2018上边发表的一篇关于索引学习的论文。索引在加速数据访问上可谓应用广泛，B-Trees是范围查询的极佳选择，Hash-maps常被用在单个点查询领域，Bloom filters常被用来检查集合中特定元素是否存在。以上几种方式都没有考虑并应用数据的相关性或分布特征。论文提出掌握数据的分布特征将有利于优化大部分索引结构。常见的索引结构可以被看作机器学习模型，例如B-tree可以被看做一个ML模型，输入是key，然后预测key在有序集合中的位置，Bloom filter可被看作一个二分类器，用来判断给定的key在集合中是否存在。

General Idea of Learned Index Using B-tree

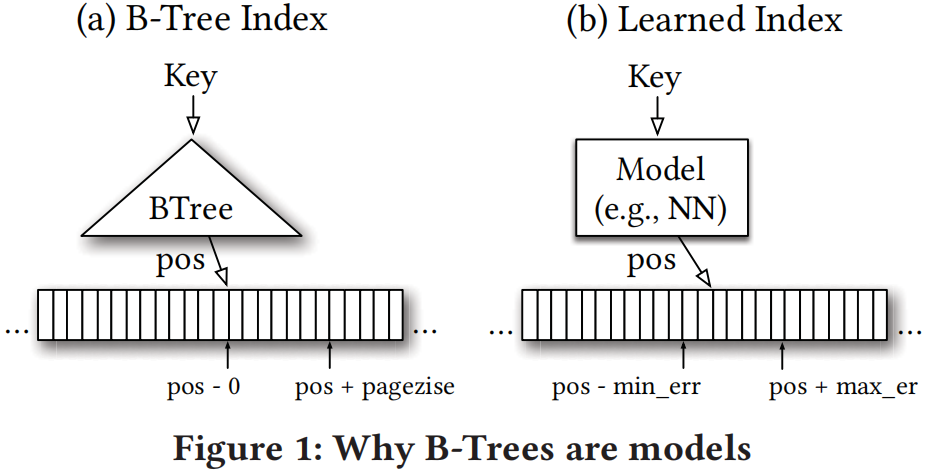
image-20221026162646208

B-Tree本身就可以被当作ML模型，回归树。其将输入的key映射到一个位置，最小误差为0，最大误差为page size。对于新数据，B-Tree需要被重新平衡，即模型需要被重新训练以提供不变的误差保证。还有一些其他的机器学习方法可以使用，例如神经网络，其可以学习多种不同的数据分布类型。挑战是如何平衡模型的复杂度以及模型的准确性。在模型复杂度方面，感性的认识是利用遍历B-Tree的时间，ML模型可以执行多少操作。以及，ML模型需要提供何种准确度才能比B-Tree模型更高效。

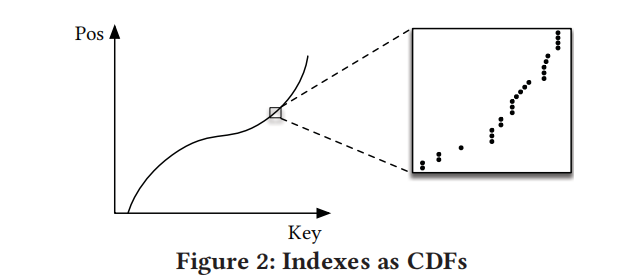
对于范围索引，数据都是有序的，我们可以利用数据累积分布函数来预测有序数组中给定key的位置：

$F(Key)$的返回值是[0,1]，表示对应的key在数据分布中大概位置的百分比，$N$表示数据总量，两个值相乘得到key在有序数组中的大概位置。B-Tree通过构建回归树学习数据分布，线性回归模型通过最小化线性函数的平方误差学习数据分布。

image-20221026164424928

为了更好的训练ML模型代替B-Tree，作者提出了学习索引框架（LIF）、递归模型索引以及基于标准误差的搜索策略。

Learning Index Framework(LIF)

LIF可以被当作一个索引合成系统，对于特定索引，LIF产生不同的索引分布，并自动对其进行优化测试。LIF可以动态地学习简单模型例如线性回归模型，其依赖Tensorflow实现推理。给定一个训练好的Tensorflow模型，LIF自动从模型中提取参数并基于特定模型产生高效的C++索引结构。（关于LIF论文介绍的很少）

Recursive Model Index

正如在第2.3节中所概述的，建立替代的学习模型来取代b型树的关键挑战之一是最后一英里搜索的准确性。为了解决这一问题作者提出了递归回归模型RMI。RMI是一个层次化模型，每个阶段模型都以key作为输入，输出将决定下一阶段挑选哪一个模型直到最后一层的结果作为最终key所在位置的预测结果。记$f(x)$表示模型，$y \in [0,N)$表示模型预测的key的位置。假设每一个stage$\ell$有$M_{\ell}$个模型，stage0训练$f_0(x)\approx y$。stage$\ell$的第$k$个模型表示为$f_{\ell}^{(k)}$，训练的损失函数为：

其中$f_{\ell-1}(x)=f_{\ell-1}^{\left(\left[M_{\ell-1} f_{\ell-2}(x) / N\right]\right)}(x)$表示上一层的输出决定对应的key将放到下层哪个模型中训练，$\left[M_{\ell-1} f_{\ell-2}(x) / N\right]$表示$x(key)$在第$\ell-2$层经过模型输出后应该进入第$\ell-1$层中的第几个模型训练。如果最后一层不能很好的学习数据分布，可以用传统的B-Tree代替。

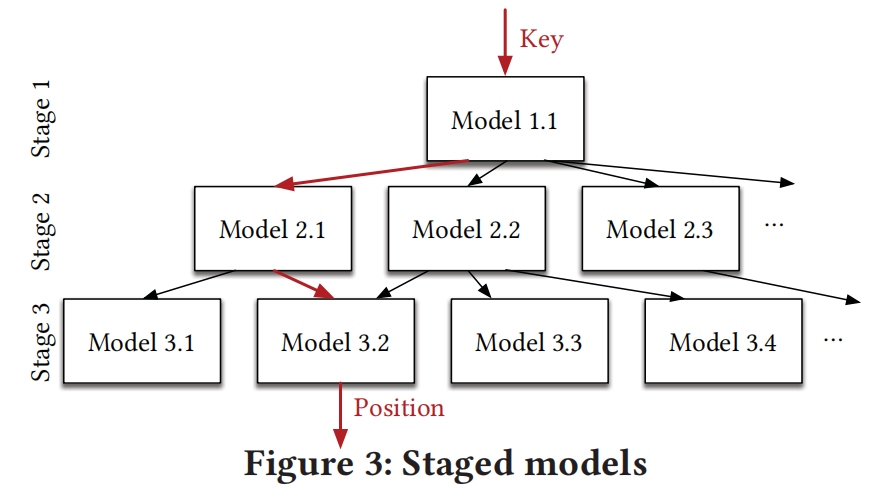
image-20221026165851679

一般第一层使用NN网络，其余层使用LR模型。当给定了stage层数，每层的模型数量，混合索引结构的训练过程如下图所示。其中第11-14行会将最后一层学习的模型计算误差，如果误差大于设定的阈值则将这一节点的模型替换为传统的B-Tree索引。因此混合索引将模型的最大误差约束在完全使用B-Tree索引之下，在最极端的数据分布下学习索引无法有效学习到数据分布，此时混合索引中全部为B-Tree索引。

image-20221026183337195

Search Strategies and Monotonicity

与传统B-Tree相比（得出key所在的page），学习索引可以直接预测出key的位置而不是区域。作者阐述了两种搜索策略：

  • Model Biased Search：和传统的二分查找类似，唯一不同在$middle point$设置为模型预测得到的位置；
  • Biased Quaternary Search：三分查找，不同的是先用模型预测出大概位置$pos$然后将初始的三个点设置为$pos-\delta, pos, pos+\delta$；

此外作者也提到了对于string的处理主要涉及怎么讲字符串转化为可供模型学习的特征，涉及到tokenization这一关键步骤，这也是未来工作的方向之一。

Learned Hash Map

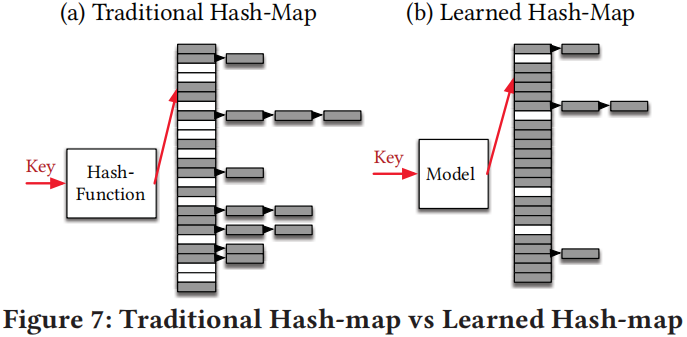
image-20221026192752171

任何Hash-map实现都要避免过多不同的key被hash到相同位置，即尽量减少碰撞。学习数据的CDF是学习更好hash函数的潜在方法。我们利用Hash-map大小M缩放CDF，$h(K)=F(K)*M$其中$K$为hash函数，如果模型$F$很好地学习了数据的CDF碰撞应该是不存在的。对于非常小的负载应用标准hash-map的Cuckoo-hashing仍然是最好的选择，对于大负载，使用学习hash函数的chained-hashmap或许更快。对于冲突处理代价较高的场景，例如需要在远程机器上进行查找，每次碰撞冲突都需要额外的RDMA，这是很费时的。

Learned Bloom Filter

image-20221026192843673

存在性验证主要使用的就是Bloom Filter。对于Bloom FIlter来说，一个好的hash函数应该做到以下几点：

  • 对于存在的key以及不存在的key，hash碰撞越多越好，因为这样使用更小的bitmap便可以表示更多的key；
  • 对于存在的key和不存在的key之间，hash碰撞越少越好，这样可以降低假阳率；

对于non-key，作者介绍了几种神经网络方法用来生成（不是太懂具体怎么生成的），将存在的key集合记做$\kappa$,不存在的key记做$\mu$，然后介绍了两种方法使用学习模型构造存在性索引：

  • Bloom Filter as a Classification Problem：

    将判断一个key是否存在视为一个基于概率的二分类问题，我们想要学习得到的模型预测给定的key是否存在。例如对于strings我们可以训练RNN或者CNN，$\mathcal{D}=\left\{\left(x_i, y_i=1\right) \mid x_i \in\right.$ $\mathcal{K}\} \cup\left\{\left(x_i, y_i=0\right) \mid x_i \in \mathcal{U}\right\}$，损失函数为$L=\sum_{(x, y) \in \mathcal{D}} y \log f(x)+(1-y) \log (1-f(x))$。$f(x)$的输出可看作x在数据集中存在的概率，我们可以设置一个阈值$\tau$，如果输出大于阈值则视为存在，若小于阈值，我们为这部分key单独构造溢出Bloom filter，查询流程如图9c。对于如何确定$\tau$才能使得学习得到的Bloom Filter具有令人满意的假阳率 ，我们将模型的假阳率记为，是不存在key的集合。溢出Bloom Filter假阳率为$FPR_B$，则系统总体的假阳率为，令，则，我们可以调参使得$\tilde{\mathcal{U}}$上的假阳率达到。（这一部分对于假阳率为什么设置为这一具体值，作者并没有细说依据）

  • Bloom Filters with Model-Hashes：

    另一种方式为学习一个hash函数使得key和non-key内部的碰撞率最大化，key和non-key之间的碰撞率最小化。 $d=\lfloor f(x) * m\rfloor$，训练$f$使得大部分存在的key被映射到更高的位置，non-keys被映射到低位置(图9b)。

Conclusion and Future Work

很多high level层面的介绍，对比了几种学习索引和B-Tree的性能提升。作者也提到了未来的几个研究方向：

  • 其他ML modeling；
  • 多维度索引，为数据引入更多特征；
  • 从学习算法的角度优化；
  • GPU/TPU;